https://www.bilibili.com/video/av22727915/?p=1

 

线性代数这门课主要描述这样的问题，

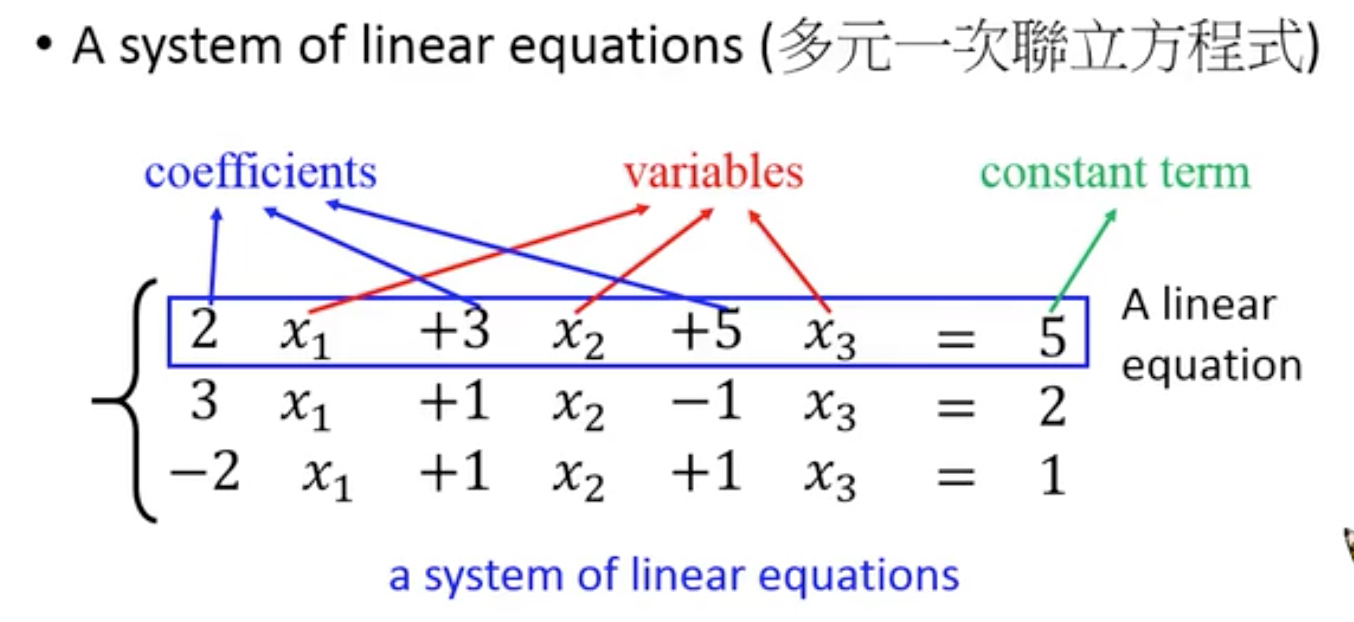
如何解多元一次方程组，即一个线性方程式的系统

解这个系统，就是要回答下面的问题，有没有解，多少解，怎么求解

 

为什么要研究一次线性方程组，因为他等价于线性系统，而线性系统是非常通用和重要的系统

什么叫linear system，如下定义

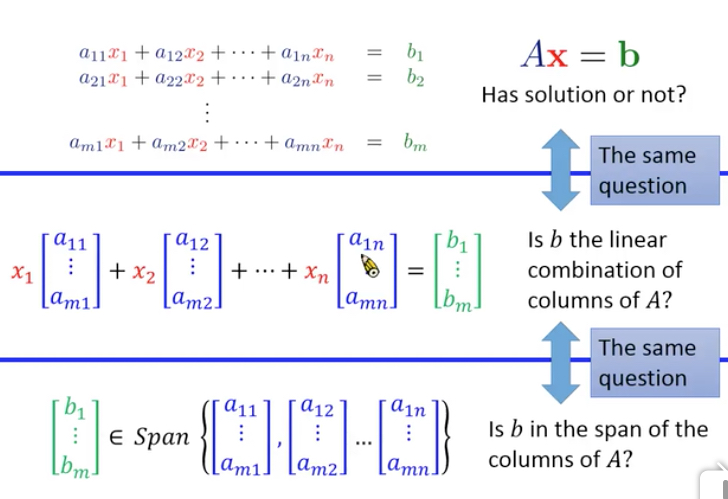
一个线性方程组，或线性系统，可以写成vector和matrix的乘积

那么这个线性方程组是否有解？

这个问题可以换种方式表达，线性组合（linear combination），span

线性组合的定义，很简单

span的定义，就是一组vector所有线性组合的总和

是否有解这个问题，可以用线性组合和span来表示？

如果有解，有几个解？要不唯一解，要不无数解

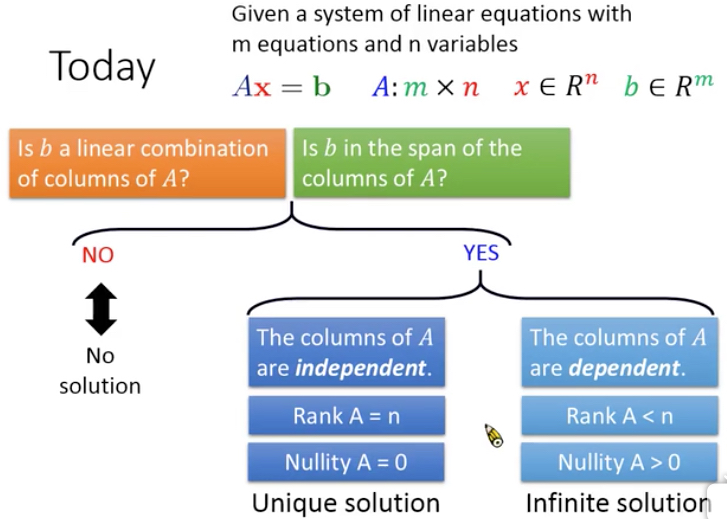
通过线性独立，线性相关，Rank和nullity这些概念来判断，

那么如何求解？

求解基于的假设是我们有些线性方程式系统是等价的

所以通过转换，可以把要求解的方程式系统转化成simple的system，如下过程，就可以完成求解

形式化的描述，我们先把方程式变成augmented matrix

然后转化过程如下，

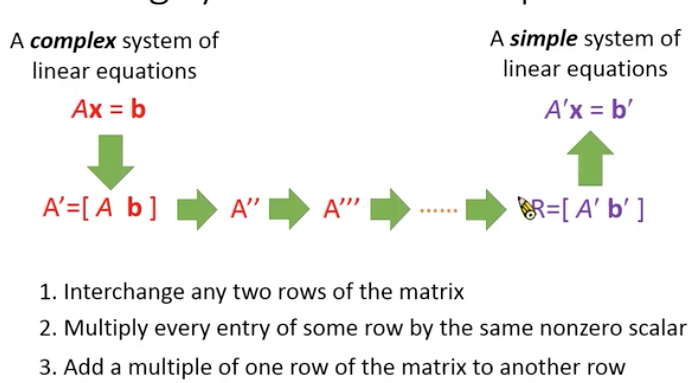
那么什么才能成为一个simple的系统了？

他如果是一个reduced row echelon form，那么就是一个可以容易求解的simple系统

左边是Row Echelon Form的定义，首先，非0行要在全0行上面，再者，leading entires(每行第一个非0值)是echelon form，从左到右阶梯排列

右边是reduced Row Echelon Form，加上一个条件，所有包含leading entires的列都是standard vectors

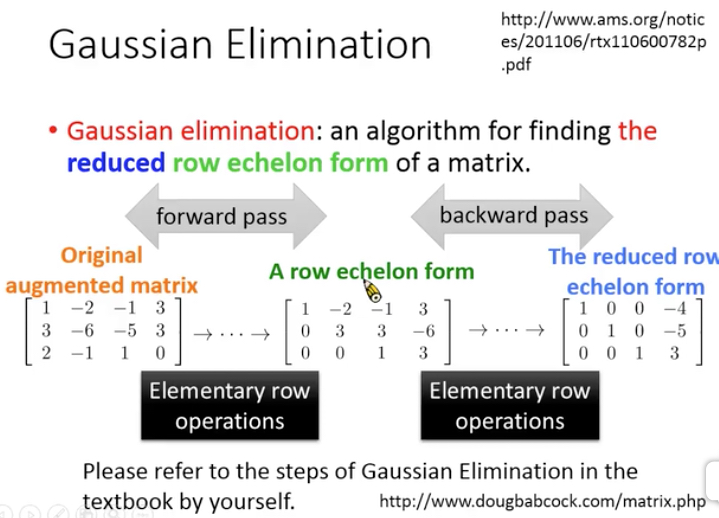
对于一个矩阵，我们如何可以求出reduced Row Echelon Form

用Gaussian Elimination, 高斯消去法，

 

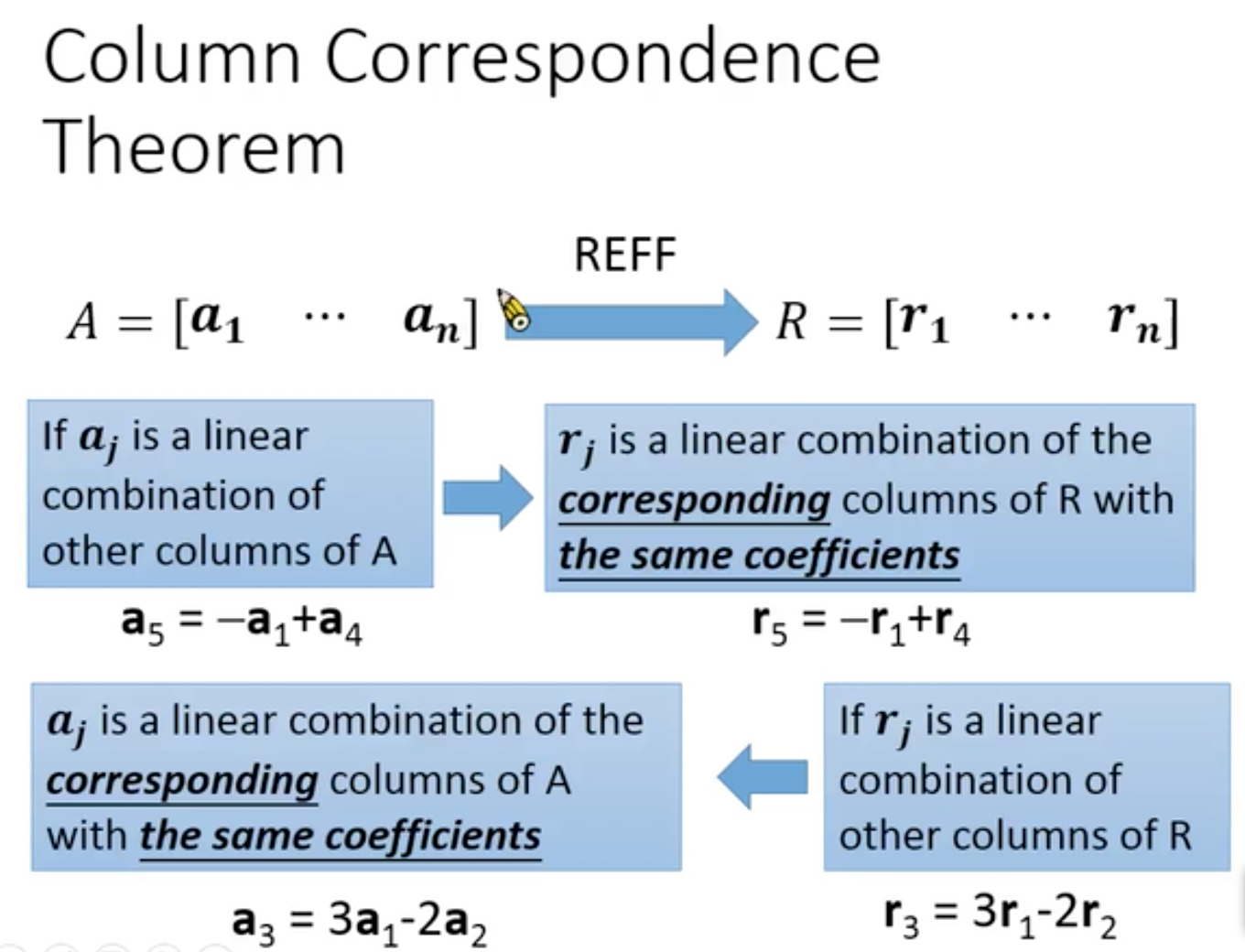
RREF vs Linear Combination

REFF变换是不会改变列向量相关性的，但会改变列向量的span

REFF变化会改变行向量的相关性，但是行向量的Span不会改变，Span意思是所有行向量的所有线性组合的集合

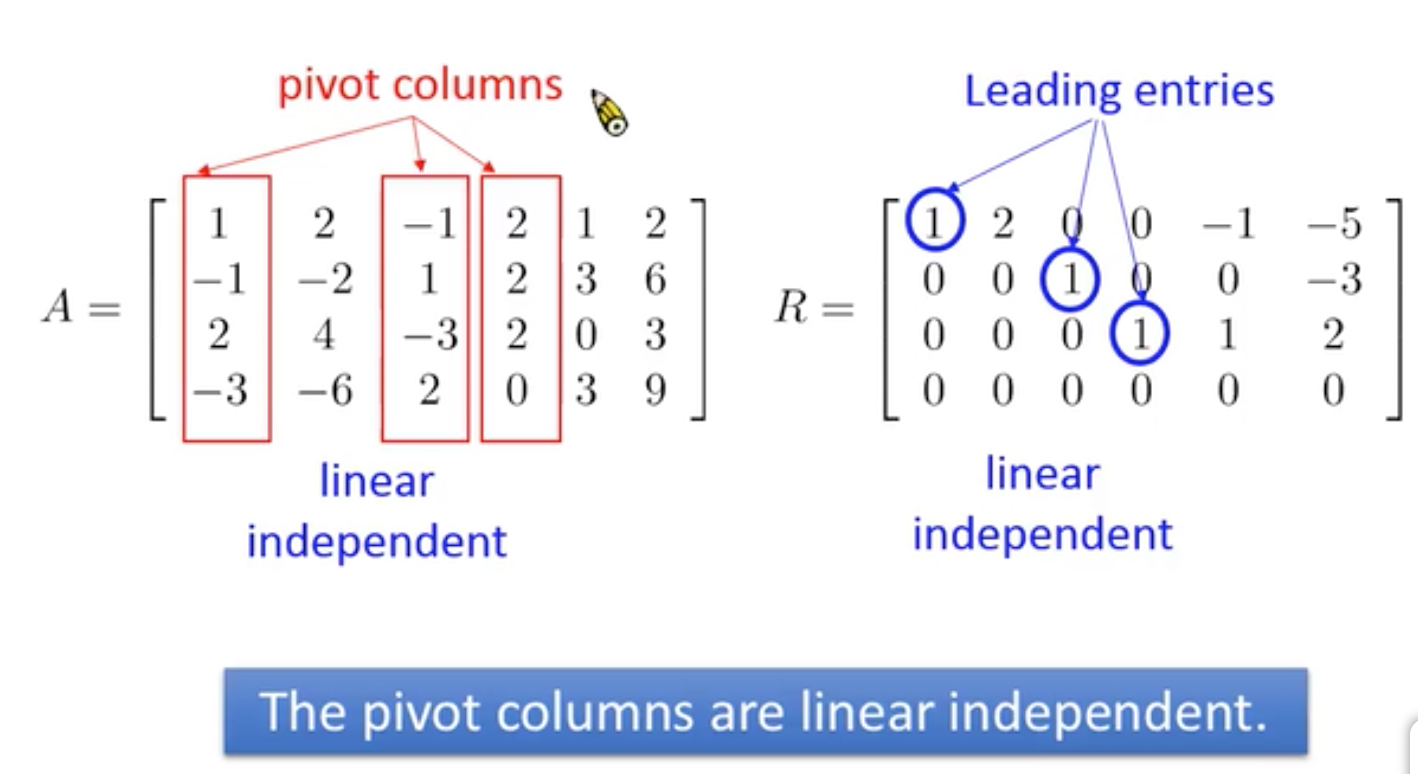
REFF vs dependent

前面REFF的定义，所有包含leading entires的列都是standard vectors，而包含leading entries的列称为pivot columns

前面定理说，REFF的变换是不会改变列向量的相关性

R中的leading entires所在列是standard vectors，所以一定是线性独立的，independent

所以可以证明，在A中对应的pivot columns也是independent

自然所有non-pivot columns都是pivot columns的线性组合

所以如果一个矩阵是independent，那么它的所有列，都需要是pivot columns

 所以可以得到这个直觉的定理，m维空间，多于m个vector一定是线性相关的，dependent

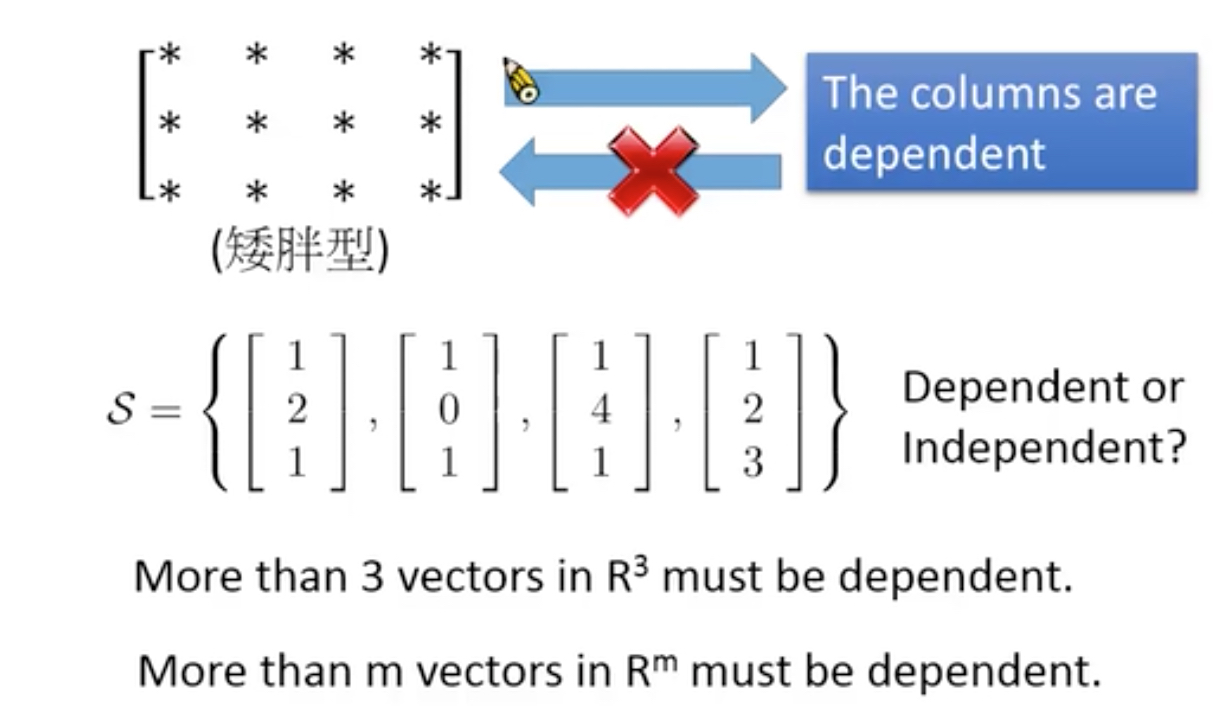
RREF vs Rank

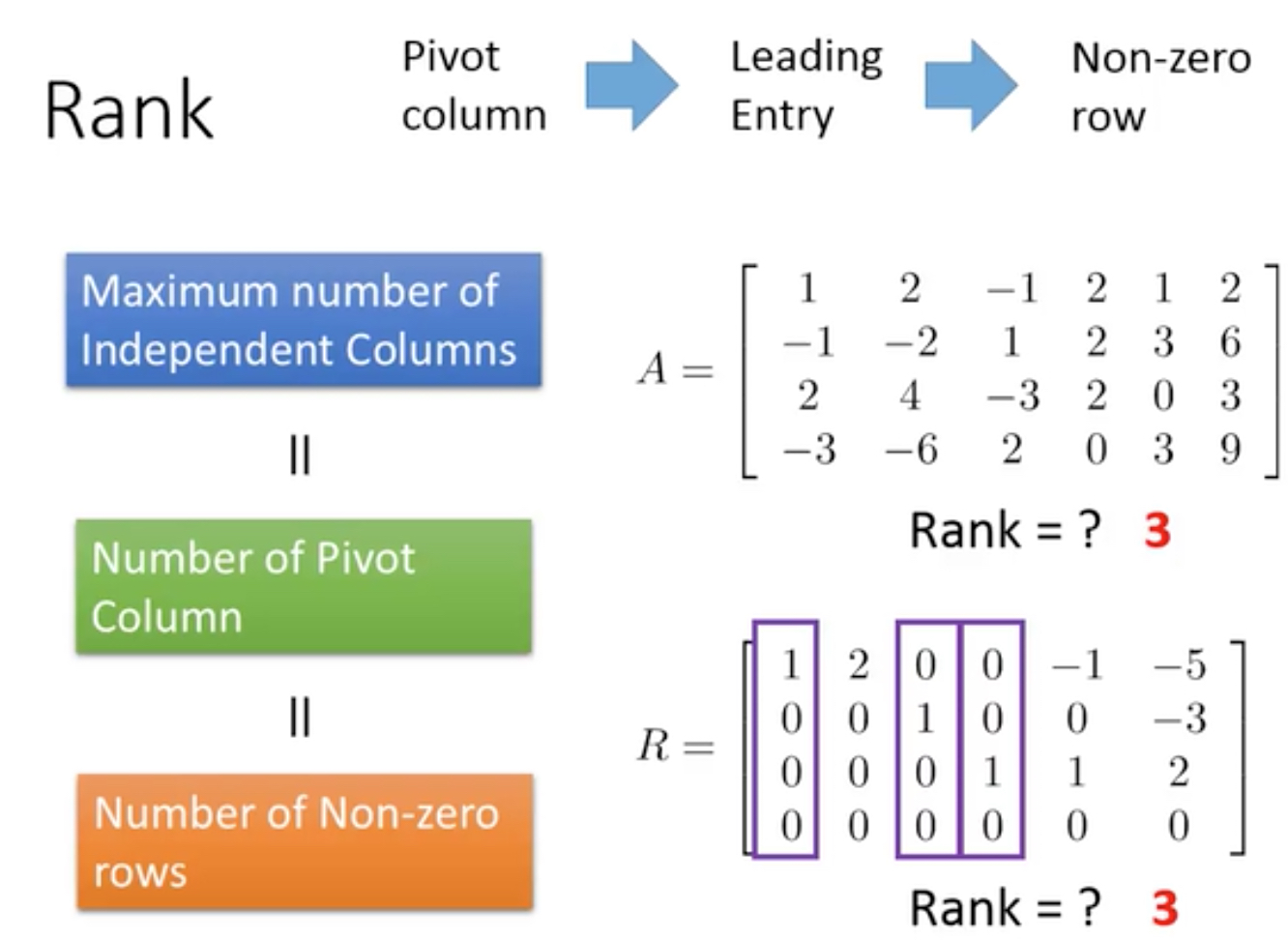
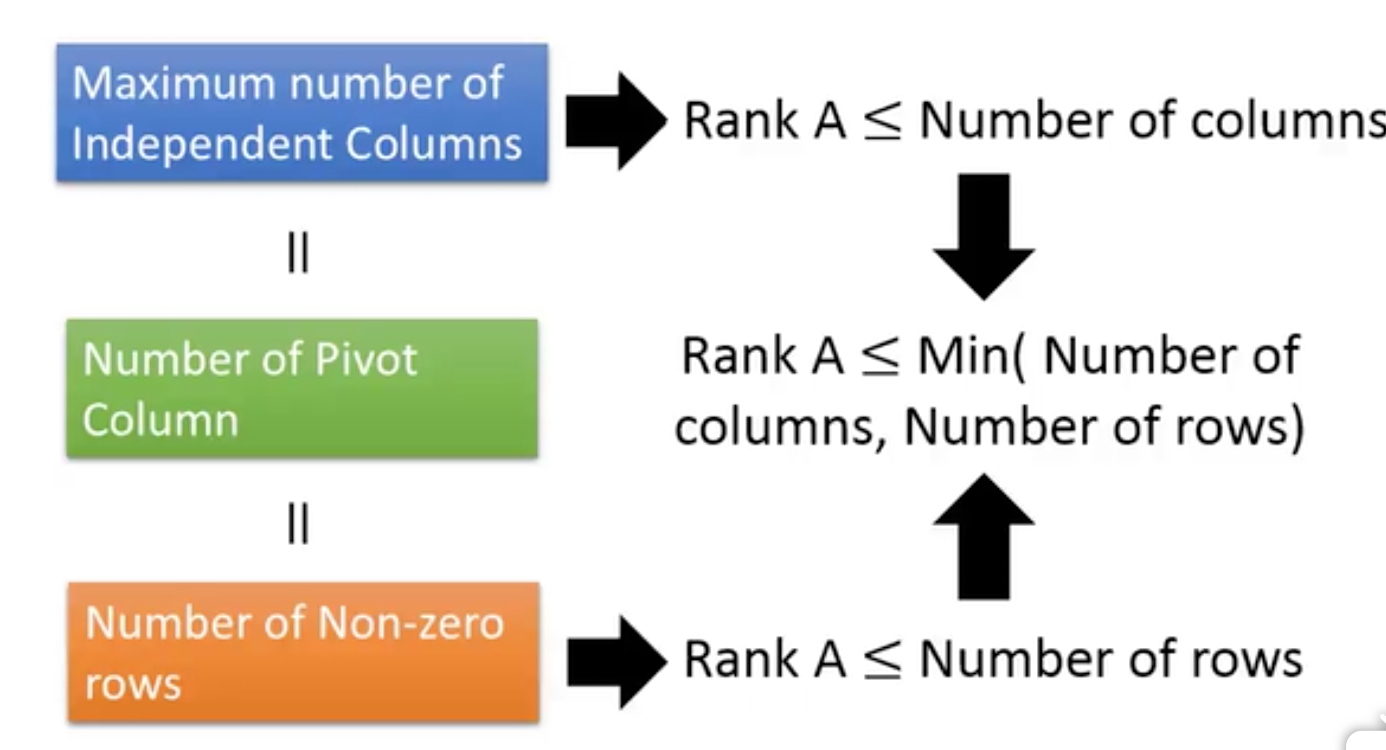
Rank，秩，的定义就是，independent columns的最大数，或pivot columns的数，或non-zero rows的数目

Rank一定是小于min(行数，列数)

Rank的特性

full rank，满秩，rank数以达到能取到的最大值

如果一个矩阵是independent，那么rank等同于columns数目

 

 定义出basic变量和free变量，和Rank的关系

basic变量就是可以确定的变量，即rank数

free变量无法确定的变量，即nullity

他们的和等同于columns的数量

 

REFF vs Span

我们讨论是否有解和Span的关系，方程式有解，意味着b在A的span里，即b可以通过A的列向量的线性组合得到

那如何更有效的判断是否有解，

如果b是可以被A的线性组合表示的，那么rank A = rank A，b

反之就无解，inconsistent

 

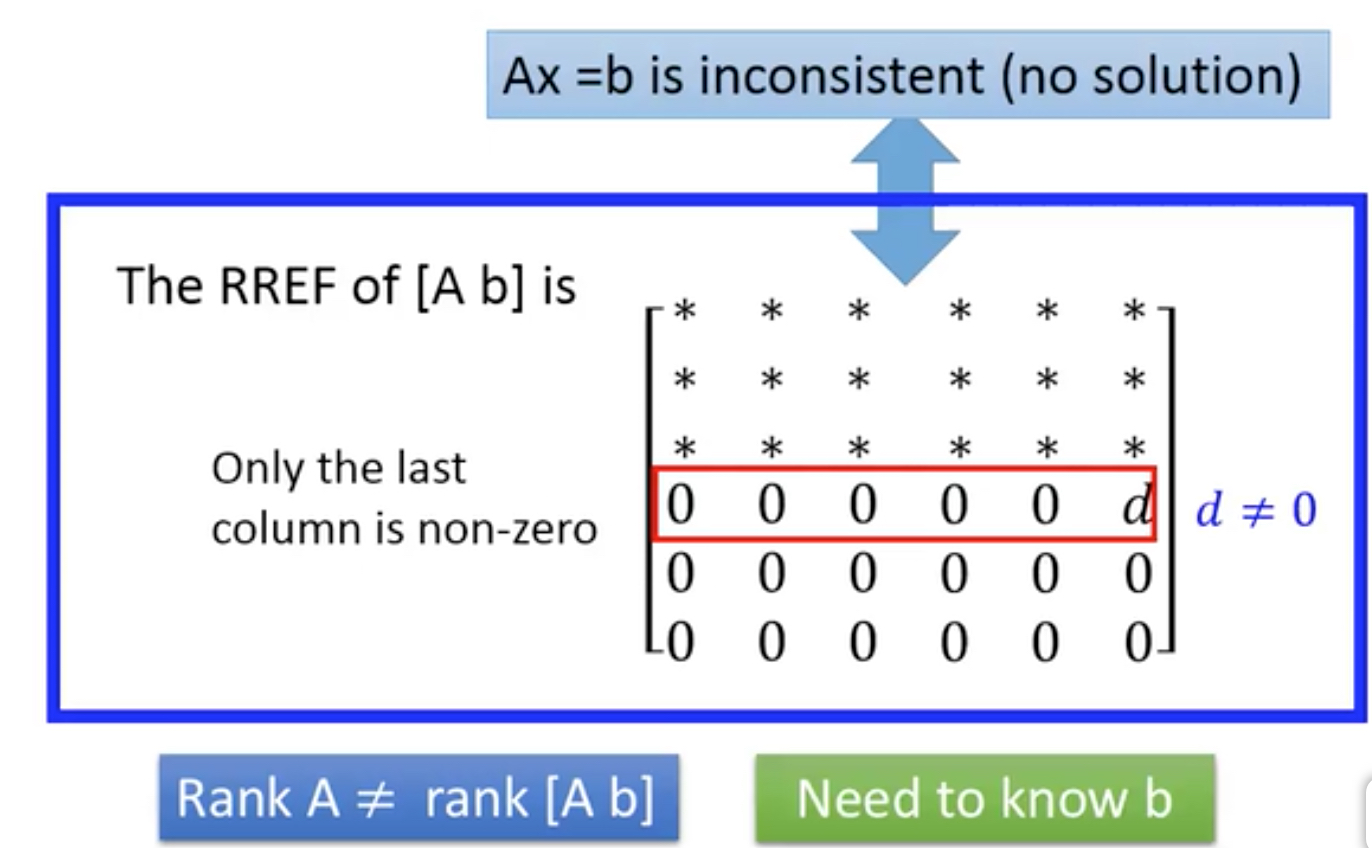
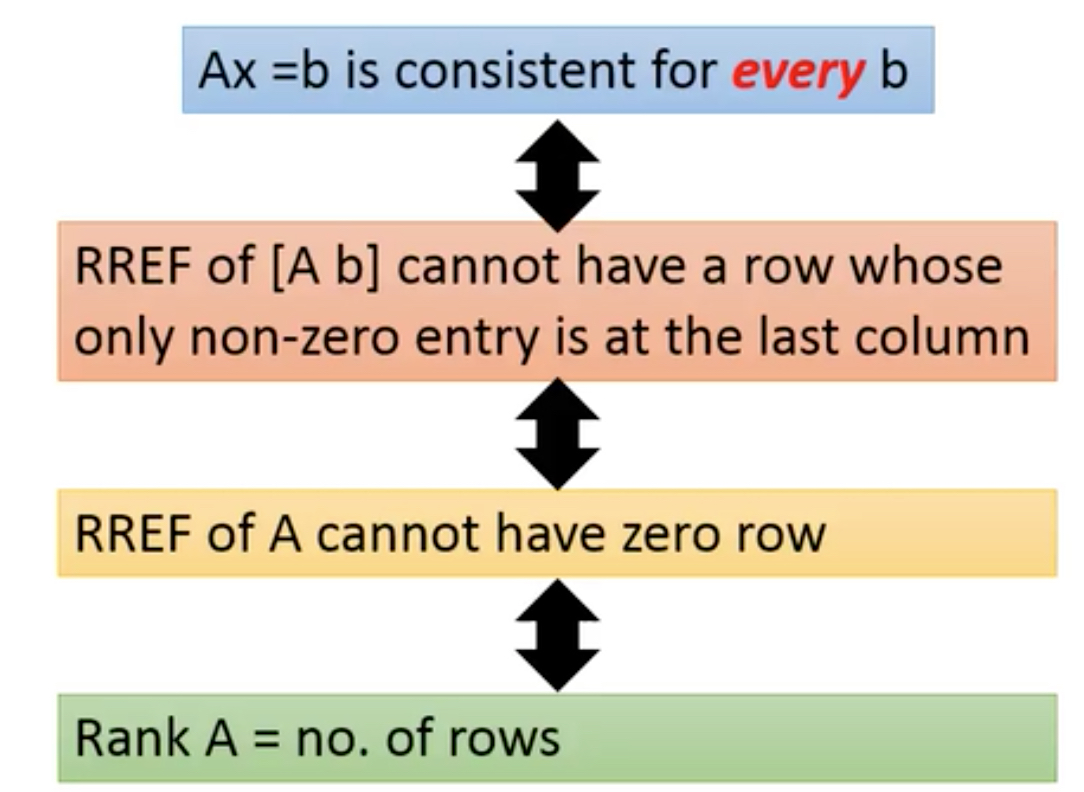
那如果要对任意b都有解，要满足什么条件？

A的REFF不能有zero row，因为对于任意b

所以rank等于行数，因为rank等于non-zero行数，而这里没有zero row

对于b都有解，意味着A的span代表整个n维空间

 如下图，如果Rank A = m

那么对于m维空间中的任意b，至少有一个解

如果rank A = n，也就是说，所有columns都是independent，最多一个解

 

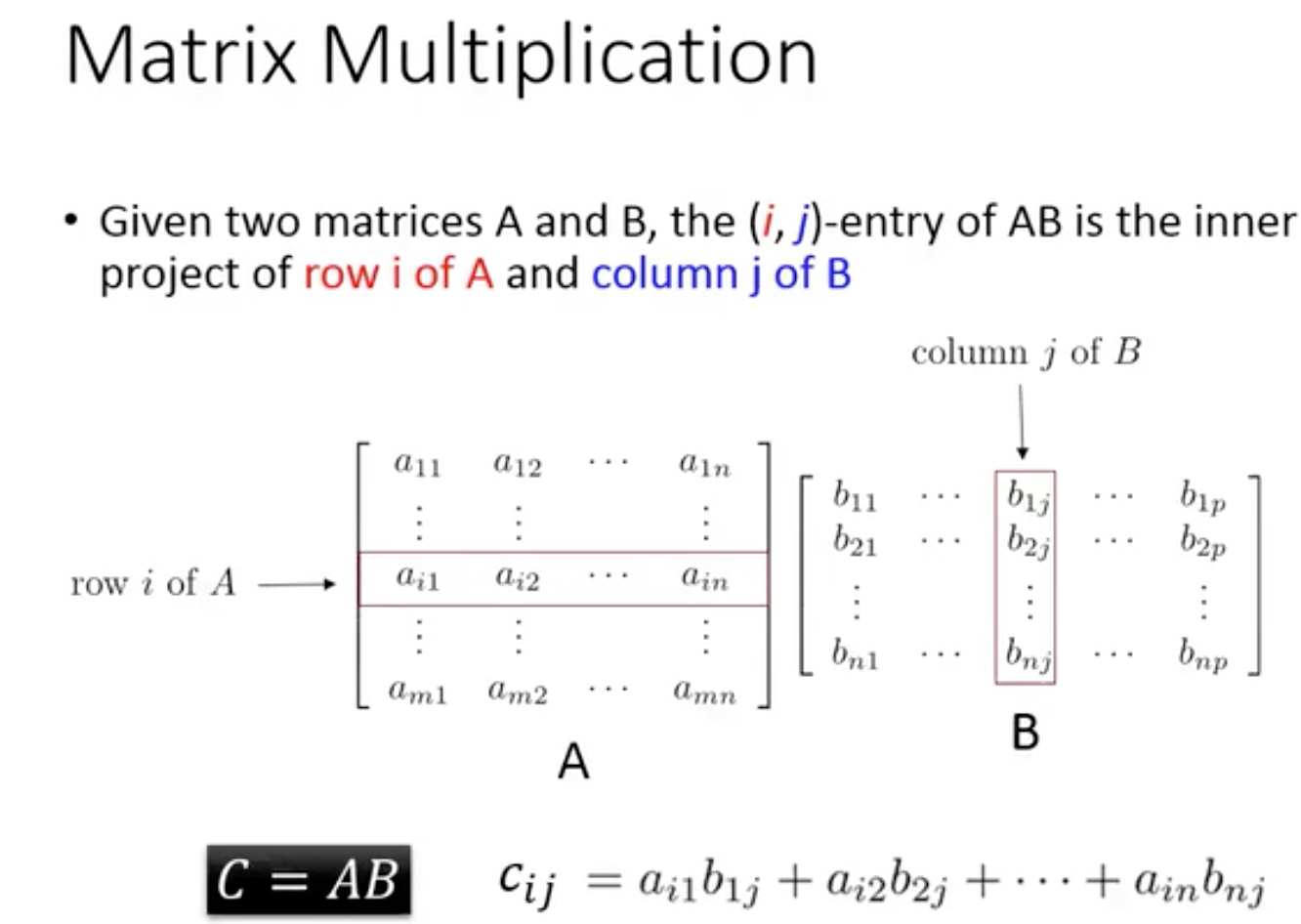
矩阵乘法

 

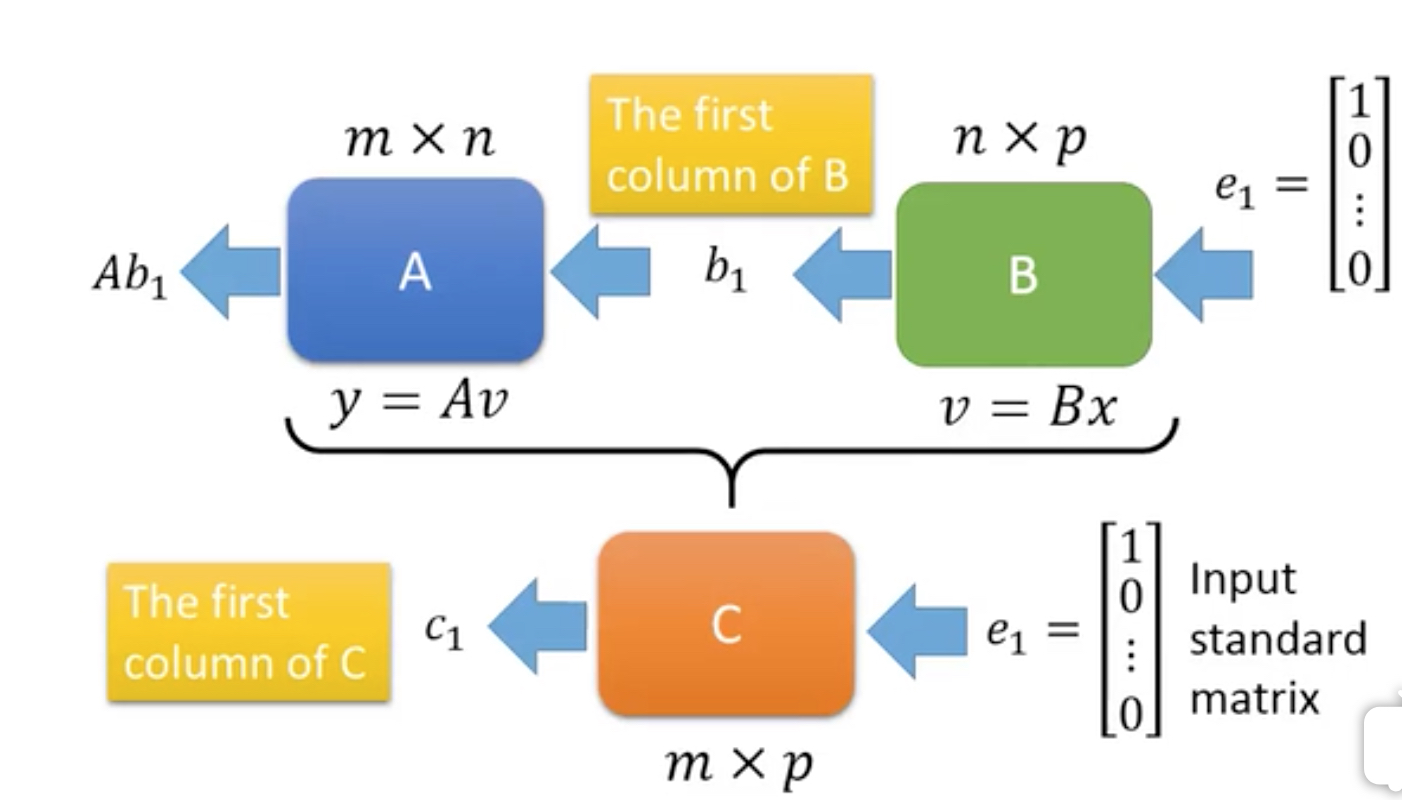
怎么理解，可看成两个矩阵的串联，这里可以用standard向量去尝试一下

矩阵乘法的一些特性

 

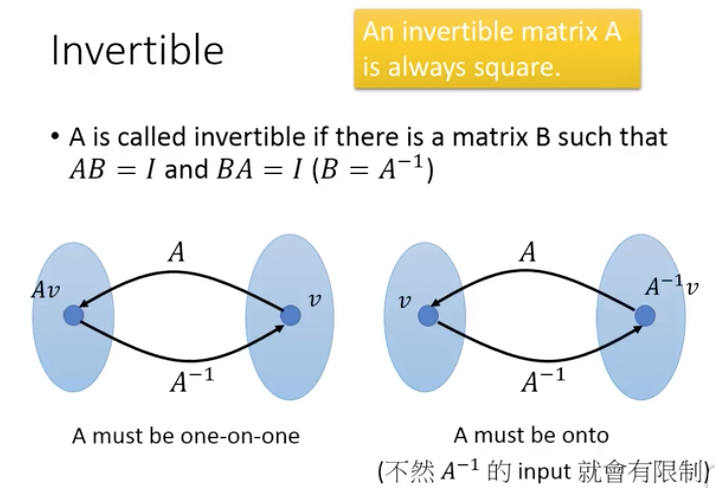
Matrix Inverse

matrix inverse的简单的定义，

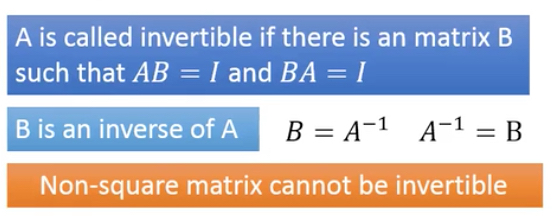
那么matrix inverse有什么用，理论上看，可以用于求解，实际上没用，因为求矩阵逆要先求RREF

 

给出矩阵逆的正式定义，

要理解红色和蓝色部分，首先要理解，function的one-on-one，onto

 

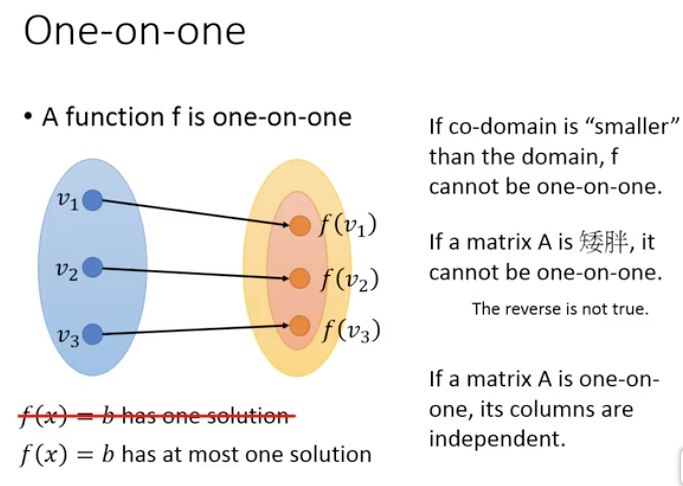
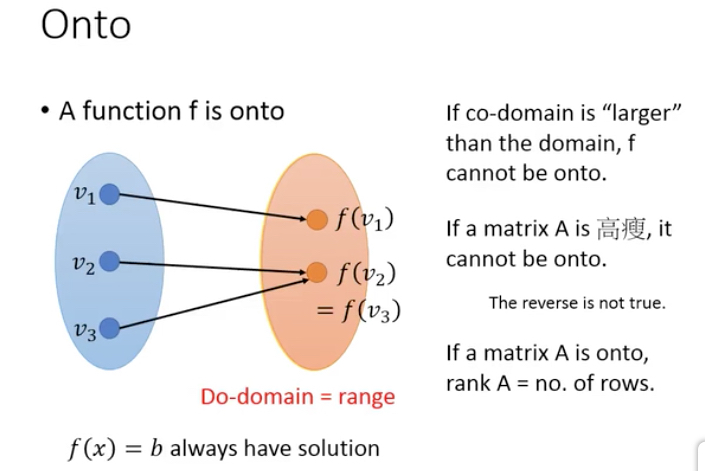
解释一下，3元一次方程组，3*3的矩阵，3个x，输出3个y

那么定义域就是整个三维空间

对应域也是整个三维空间，值域可能小于对应域，因为有些值可能取不到

one-on-one，最多一个解，可能没有解，如果b落到值域外，这种情况所有columns肯定都是independent的

onto，一定有解，即值域等于定义域，rank等于行数

如果matrix可以inverse，需要既是one-on-one，也是onto

 

再来理解，这一句，

“A is a product of elementary matrices”

什么是elementary matrices？

如左一图，前面知道，对矩阵做下面3中row操作，不会改变矩阵的解集合

而每一种row operation，都可以用一个elementary matrix表示

那么怎么找到row operation所对应的elementary matrix？

答案如中间的图，对identity矩阵做相应的row operation，得到的矩阵就是elementary matrix

elementary matrix的好处在于，对它求inverse是非常简单的，如右图

对应任意一个A，可以通过一系列的row operation变成RREF

左边的图，当一个矩阵可逆，它的RREF会是identity矩阵

所以可以推导出，如果矩阵可逆，它的逆就这一堆elementary matrices的乘积

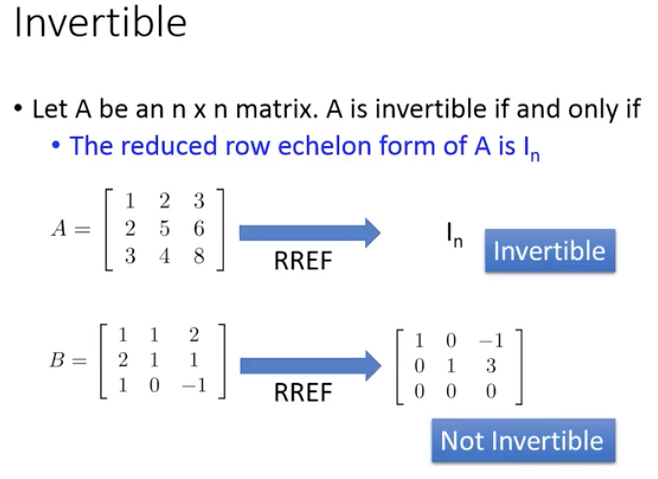
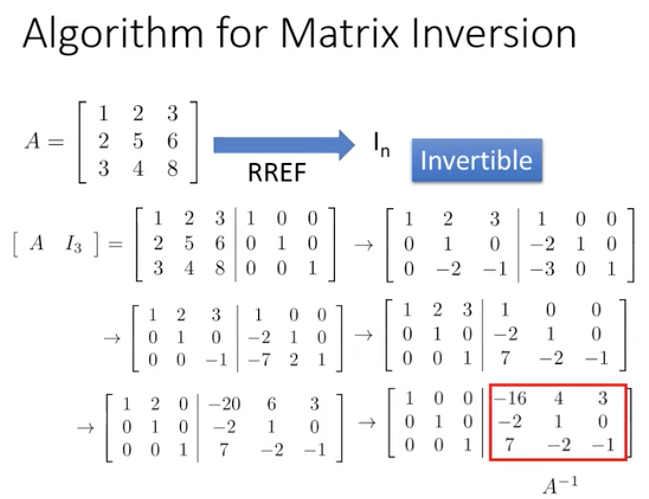
 好理解完了，实际中，我们是怎么来求矩阵逆的？

如下图，看那个例子应该很清楚，把A和I放一起，row operation，如果A变成I了，那么后面的B就是A inverse

 

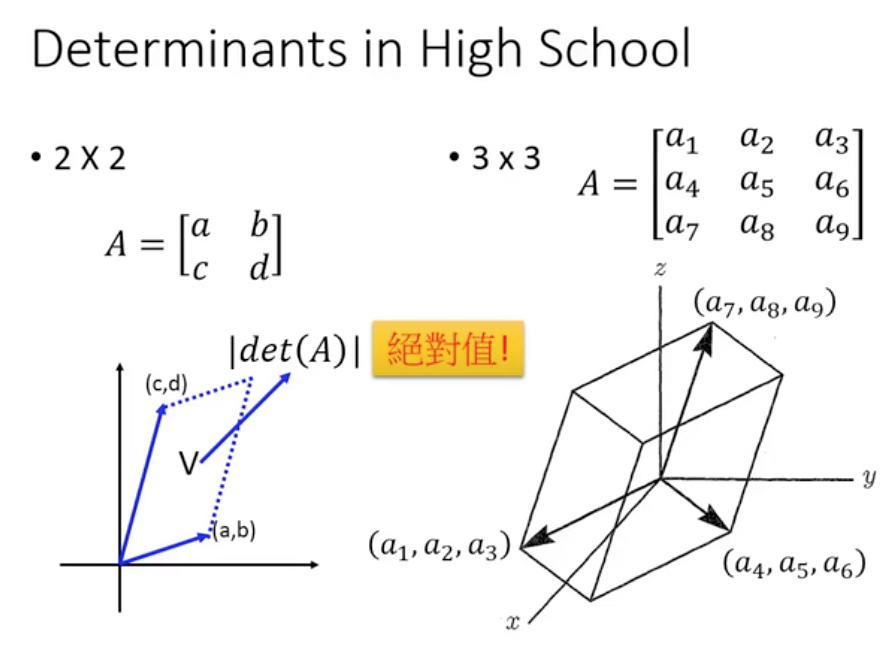
Determinant，行列式

简单的看下，什么是determinant？

determinant有什么几何意义吗？

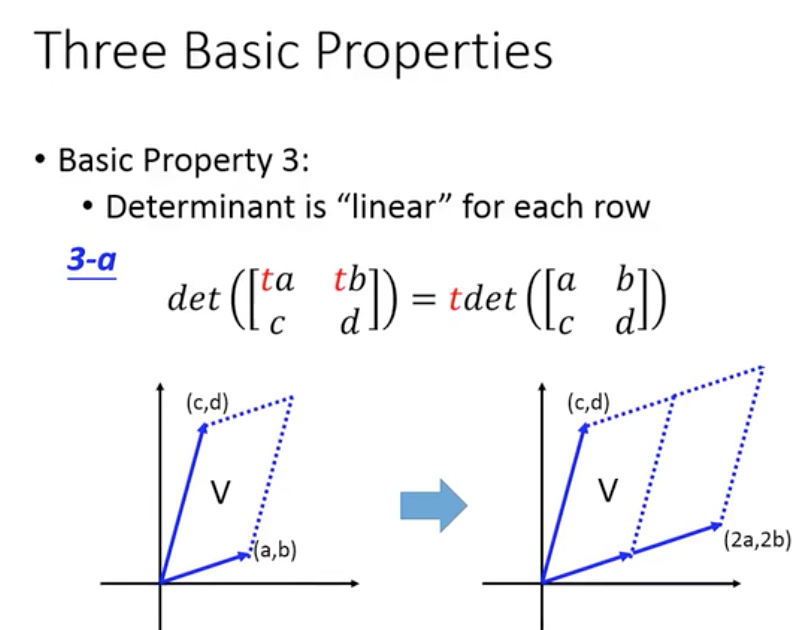
Determinant有什么基本特性？

1. 任何Identity矩阵的det=1

2. 交换任意两行，会改变det的符号；所以如果有两行相等，det=0

 3.  Det对于每一行都是线性的；这个很有意思，可以推导出下面几个有用的推论

 

Determinant的其他特性？

 

Determinant和可逆之间的关系？

A可以通过RREF转化成R，A和R的Det之间关系如下，因为RREF的操作，只会改变符合和乘以倍数

所以可以推导出，可逆意味着det不为0

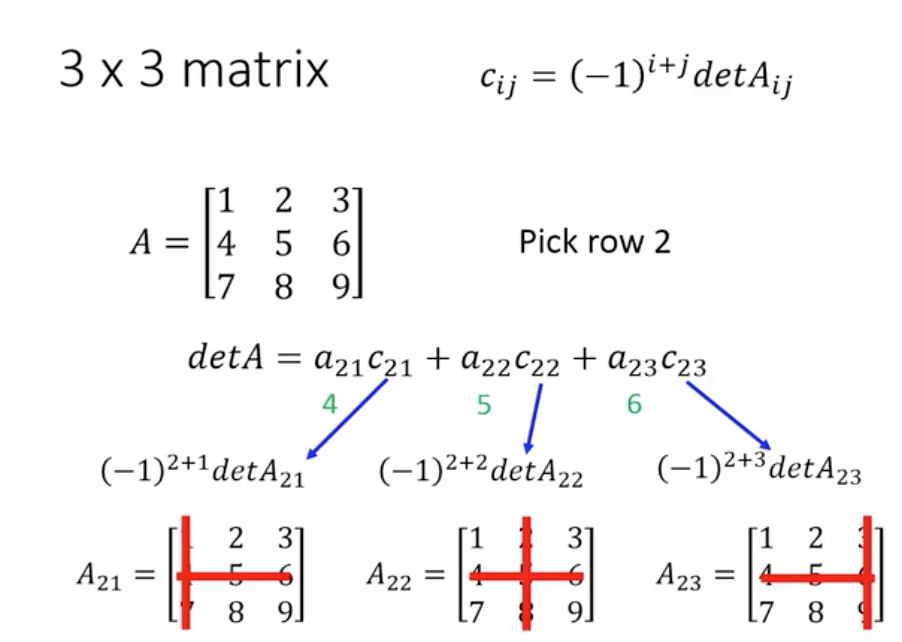
Determinant的正式定义

这个看着比较难理解，通过任意一行或列，乘上cofactor都可以算出det

而cofactor需要计算相应A的det，而算A的det又需要继续分解，直到分解的A是2维或3维行列式可以直接计算

看个计算过程的例子，

 

Subspace

先看下什么是subspace，子空间

从定义上看，对于一个vector集合中任意向量的线性组合得到的向量仍然在这个集合中，这个集合就称为subspace

简而言之，对线性组合闭合的，线性组合的闭包？

根据span的定义，vector集合的span一定是subspace

一些特殊的subspace，

Null space是A的解向量的集合，Column和Row Space很容易理解

所以这里对于是否有解，又有一种新的说法，b在A的Column space里面

 

Subspace的basis

basis有两点定义，independent和能够通过basis生成整个R

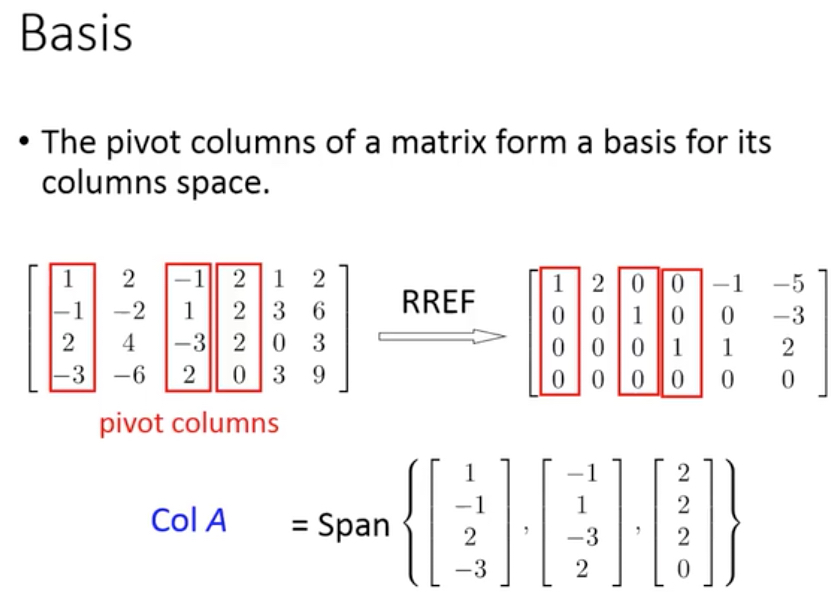
basis有几个特性，

最小的generation set，再小不可能生成整个空间R

最大的independent vector集合，

一个subspace可能有多个basis，但是他们的number是一样的，number称为空间的dimension

所以几维空间，使用basis的number决定的

ColA，NullA，RowA

下面的图更形象的表示各个subspace的含义

 

下面看看各自的basis和dimension，

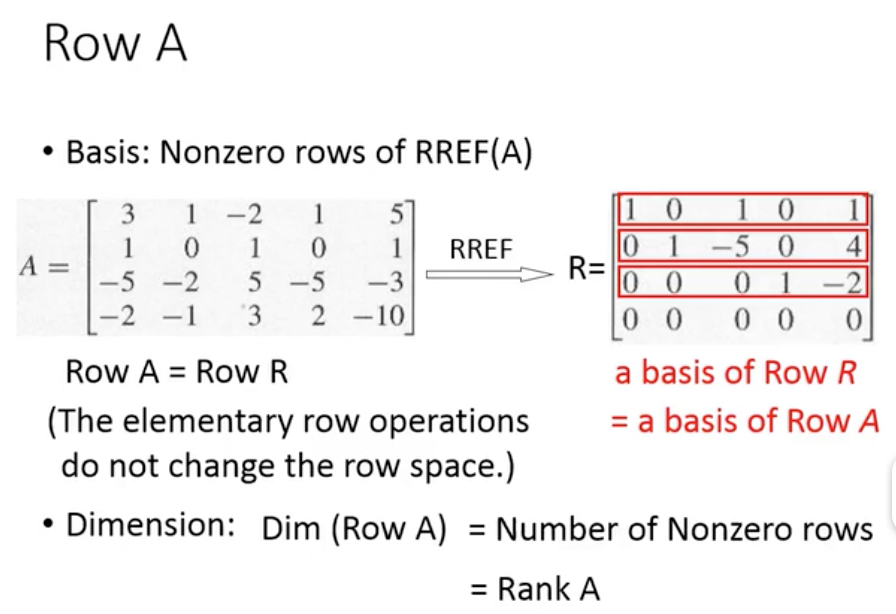
从而可以得到dimension理论，

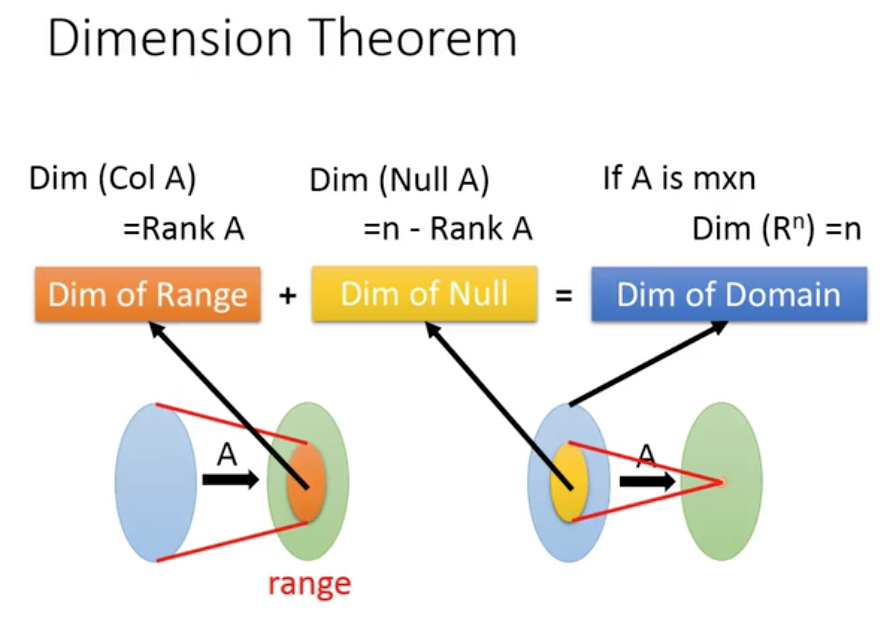
Summary